Estudamos dois tipos de progressões: aritmética e geométrica. A aritmética é percebida quando cada termo aumenta ou diminui uma mesma quantidade, assim de diminuirmos um termo do seu anterior teremos a nossa razão. Já a geométrica é percebida quando os números aumentam pela multiplicação de uma constante, assim se dividirmos um termo pelo seu anterior teremos a nossa razão.
Exemplos de PA:
A) (1, 2, 3, 4, ...) em que a razão é 1
B) (-10, -5, 0, 5, ...) em que a razão é 5
Exemplos de PG:
A) (1, 3, 9, 27, ...) em que a razão é 3
B) (100, 50, 25, ...) em que a razão é 0,5
Vamos fazer um resuminho sobre esses dois tipos para auxiliar na hora dos exercícios. Lembre que este assunto é bem frequente tem vestibulares, e bem simples de se entender. Vale a pena gastar um tempinho trabalhando em cima disto. Confira!
PROGRESSÃO ARITMÉTICA
Finita: (a1,
a2, a3, ... , an)
Infinita: (a1,
a2, a3, ... )
Razão:
denominamos razão “r” a diferença entre um termo e seu antecessor: a2
– a1, a3 – a2, ... , an – an-1.
Termo geral: determinamos qualquer
termo através desta fórmula. (Também pode ser usada para descobrir a
razão, quando temos um termo qualquer e o primeiro termo; para descobrir o
primeiro termo, quando temos a razão e outro termo qualquer)
an
= a1 + (n – 1) ∙ r
Soma dos termos (P.A. finita):
calculamos a soma de todos os termos ou dos n primeiros termos.
Três termos em P.A.: podemos escrever
três termos seguidos de uma sequência da seguinte forma: (note que assim os três termos ficam
em função de um só e da razão, possibilitando que possamos calcular as
variáveis ainda não conhecidas)
(an-1,
an, na+1) = (x – r, x, x + r)
Observações:
OBS. 1) A razão
da P.A. dos números pares é 2.
OBS. 2) A razão
da P.A. dos números ímpares é 2.
OBS. 3) A razão da P.A. dos números
múltiplos de n é n. (Ex: múltiplos de 5 tem razão 5,
múltiplos de 300 tem razão 300)
OBS. 4) Se soubermos um termo qualquer
e a razão podemos calcular ele direto, sem saber o primeiro termo.
Por exemplo: Se a4 = 3 e a
razão é 2, qual é o a50?
Pelo índice temos que de 4 até 50 se somaram 46 razões,
então:
a50 = a4
+ 46 ∙
r
a50 = 3 +
46 ∙
2 = 95
PROGRESSÃO GEOMÉTRICA
Finita: (a1,
a2, a3, ... , an) em que a1 ≠
0.
Infinita: (a1,
a2, a3, ... ) em que a1 ≠
0.
Razão:
denominamos razão “q” a razão entre um termo e seu antecessor: a2 ÷ a1,
a3 ÷ a2, ... , an ÷ an-1.
Termo geral: determinamos
qualquer termo através desta fórmula.
an
= a1 ∙ qn–1
Soma dos
termos: (P.G. finita): calculamos a soma de todos os termos ou
dos n primeiros termos.
Soma dos termos de
uma P.G. infinita:
Em que -1 < q < 1.
Três termos em P.G.:
(an-1,
an, na+1) = (x ÷ q, x, x ∙ r)
Produto de uma P.G.
limitada:
Download PDF
Aproveite e faça a lista de exercícios de PA e PG, confere aqui neste link!





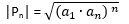





Nenhum comentário:
Postar um comentário