FORMAS GEOMÉTRICAS

          As formas geométricas estão presentes no nosso dia a dia. Muitas delas possuem formas semelhantes, por exemplo: 

• Uma laranja, uma bola de basquete, o planeta Terra... 
• Uma caixa de pasta de dente, uma caixa de sapato, um tijolo, a sala de aula... 
• Uma lata de refrigerante, um pacote de bolacha, um rolo de papel higiênico, uma vela... 
• Um cone, uma casquinha de sorvete, um chapéu de festa de criança... 

        A Geometria é a disciplina que trata do estudo das formas geométricas, e de suas principais características: sua forma, sua extensão, suas propriedades e sua posição relativa. 

         
      Apenas pelo fato de observarmos a natureza, o mundo que nos rodeia, podemos confirmar a existência e presença das mais variadas formas nos corpos materiais que convivem na natureza e, então, é dessa maneira que vamos formando a ideia de volume, superfície, linha e ponto.

1.2. SÓLIDOS GEOMÉTRICOS

          Os sólidos geométricos são figuras tridimensionais, ou seja, que possuem três dimensões: comprimento, largura e altura.
            As figuras geométricas espaciais também recebem o nome de sólidos geométricos, que são divididos em: poliedros e corpos redondos.

1.3. POLIEDROS

         Poliedros são sólidos geométricos formados por três elementos básicos: vértices, arestas e faces. Suas faces são figuras geométricas planas (triângulos, quadrados, retângulos, hexágono, etc.), suas arestas são os lados destas figuras planas e seus vértices são os vértices das figuras planas.
        Assim, temos que os poliedros permanecem sempre em equilíbrio quando deixados sobre uma superfície plana, pois todas as suas faces (ou modos de apoiar-se) são planas.

          A classificação geral dos poliedros é feita de acordo com o número de faces que eles possuem:

          O prefixo destacado em cada nome refere-se ao número de faces do poliedro. Os demais poliedros em geral, são indicados nomeando-se o total de suas faces. Por exemplo: “poliedro de 11 faces”.

POLIEDRO REGULAR 

          Um poliedro é considerado regular quando suas faces são polígonos regulares e congruentes. Ou seja, todas as suas faces são iguais, sendo polígonos regulares. Ao todo só existem 5 poliedros regulares:

            Os cinco poliedros regulares (tetraedro, dodecaedro, hexaedro (cubo), octaedro e icosaedro) já eram conhecidos no século IV a.C.

 POLIEDROS CONVEXOS E CONCAVOS

          Diz-se que um poliedro é convexo se o seu interior é convexo, ou seja, um poliedro é convexo se qualquer reta o corta no máximo em dois pontos. Caso isso não ocorra, dizemos que o polígono é côncavo (ou não convexo).

          Os poliedros também se dividem em: prismas e pirâmides.

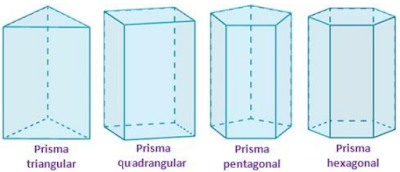
1.3.1. PRIMAS

          Os prismas são poliedros cujas faces laterais são paralelogramos e cujas bases são polígonos de mesma forma e de mesmo tamanho. Para “nomear” um prisma, basta verificar o polígono que constitui a(s) sua(s) base(s) (ex: prisma triangular, prisma hexagonal, etc). Os prismas cujas faces (tantos as laterais como as bases) são todas paralelogramos denominam-se paralelepípedos.

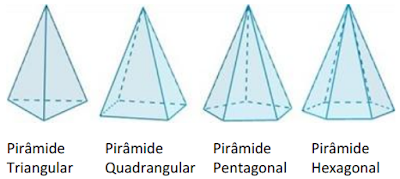
1.3.2. PIRÂMIDES

          As pirâmides são poliedros cujas faces laterais são triângulos que têm um ponto em comum. Analogamente aos prismas, para “nomear” uma pirâmide, basta verificarmos qual o polígono que constitui a sua base.

1.4. CORPOS REDONDOS

         Corpos redondos são formas geométricas espaciais que apresentam pelo menos uma parte arredondada em sua superfície.
          Veja exemplos de corpos redondos:

1.4.1. CILINDRO. 

         Cilindro é o sólido obtido por meio da união de todos os segmentos de retas paralelos à reta s que unem um ponto do círculo C (pertencente a α) a um ponto de β.

         A altura do cilindro é dada por meio da distância entre os planos das bases. A reta que passa pelo centro das bases é chamada eixo do cilindro. As geratrizes são segmentos paralelos ao eixo cujas extremidades são pontos da circunferência.

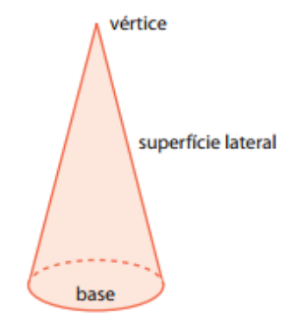
1.4.2. CONE

         Vamos considerar um plano α, uma região circular R nesse plano e um ponto P não pertencente a α. A reunião de todos os segmentos que ligam cada ponto de R ao ponto P é um sólido chamado cone circular.

         A superfície do cone é formada por uma parte plana, a região circular, que é a sua base, e uma parte não plana, “curva“, “arredondada”, que é a sua superfície lateral.

         Um cone reto pode ser obtido girando-se uma região triangular cujo contorno é um triângulo retângulo em torno de uma reta que contém um dos catetos.
         Por esse motivo, o cone reto é considerado um sólido ou corpo de revolução e é chamado cone de revolução.

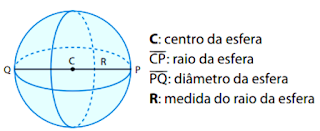
1.4.3. ESFERA

         Consideremos um ponto C e um número real positivo R qualquer.
        A esfera de centro C e raio de medida R é o conjunto de todos os pontos do espaço que estão a uma distância menor ou igual a R do ponto C.
         A “casquinha” ou a fronteira da esfera chama-se superfície esférica.